Building 3D Projections with JavaScript and HTML
In the world of web development, creating 3D visualizations used to be complex and reserved for specialized software. However, with the power of HTML5 Canvas and JavaScript, we can now bring 3D graphics directly to the web without the need for plugins or heavy external libraries.
In this article, we’ll explore how to create a 3D model (a rotating cube) and project it onto a 2D canvas using basic JavaScript. You’ll learn how to manipulate 3D points, perform rotations, and render animations right in your browser!
As an exciting bonus, we’ll also explore how to create and visualize the tesseract ( a 4D object) expanding the possibilities of spatial dimensions and animation!
Prerequisites
Before we get started, make sure you have a basic understanding of HTML, CSS, and JavaScript.
- Basic Understanding of HTML, CSS, and JavaScript: Familiarity with the fundamental concepts of HTML for structuring web pages, CSS for styling, and JavaScript for adding interactivity is essential. This tutorial assumes a basic knowledge of these languages.
- Web Browser: Use a modern web browser like Google Chrome, Mozilla Firefox, or Microsoft Edge.
For the purpose of this tutorial, you can download the source files for the demo to help you follow along:
Note: As you test the source files, ensure that you load them within a suitable environment such that all the files are loaded. For offline use, we recommend that you use Live Server and vscode to load the files. Simply open the files in Vscode and run “index.html” using Live Server.
Demo
Here is what we are going to create.
Setting Up the Project
Let's start by setting up the basic HTML structure for our project. Create an HTML called "index.html", with a basic HTML web format, and add a canvas element.
HTML5's <canvas> element allows you to draw graphics directly on a webpage using JavaScript. It's essentially a blank space where we can paint anything we like 2D shapes, images, and even 3D projections!
Creating the Canvas Element
To get started, we need a <canvas> element in our HTML file:
<canvas id="canvas" width="500" height="500" style="background: black;"></canvas>
This creates a 500x500-pixel canvas with a black background. The next step is to access this canvas through JavaScript and set up a 2D rendering context for drawing.
Also, add a script tag for our javascript code, and you are good to go!
Here is our full code template.
<!DOCTYPE html>
<html lang="en">
<head>
<meta charset="UTF-8">
<meta name="viewport" content="width=device-width, initial-scale=1.0">
<title>3D Projection</title>
</head>
<body>
<!-- Create a canvas element to draw on -->
<canvas id="canvas" width="500" height="500" style="background: black;"></canvas>
<script type="text/javascript">
</script>
</body>
</html>
Understanding 3D Coordinates and Projections
In a 3D space, every point is defined by three coordinates: x, y, and z. But since we’re working with a 2D canvas, we need to "flatten" these 3D points into 2D to display them. To do this we need to do a projection.
The Concept of Perspective Projection
To simulate the depth of 3D space on a 2D canvas, we can use a perspective projection. This means objects farther from the viewer will appear smaller. Here’s the basic formula for projecting a 3D point onto a 2D plane:
let x2D = (x / (z + D)) * f + width / 2;
let y2D = -(y / (z + D)) * f + height / 2;Where:
x,y, andzare the coordinates of the 3D point.fis the focal length (how zoomed in/out the scene is).Dis the distance from the viewer (larger values make objects smaller).widthandheightare the dimensions of the canvas.
Lets Dive Into the Code
1.Initial Variables
First of all, we need to create some variable that will drive our simulation.
// Access the canvas element and its 2D rendering context
var canvas = document.getElementById("canvas");
const width = canvas.width; // Canvas width
const height = canvas.height; // Canvas height
var gl = canvas.getContext("2d"); // 2D drawing context
const timeout = 50; // Timeout for animation update
const f = 500; // Focal length for 3D projection (larger values make objects smaller)
const D = 500; // Distance from the viewer (larger values make objects appear smaller)
These variables will allow us to define the canvas properties, such as its width and height, and set the parameters necessary for the 3D projection. We'll also configure the focal length and viewer distance, which control how objects are rendered and scaled within the canvas. Additionally, we'll set up a timeout to regulate the animation updates, ensuring smooth and consistent rendering as we animate the rotating cube.
2. The Update Function
The update() function is the heart of the code. It’s responsible for refreshing the canvas, rotating the 3D model, and redrawing it. This function is called repeatedly using setTimeout,an inbuilt function for creating an animation loop.
function update() {
setTimeout(update, timeout); // Continuously update the canvas
}
setTimeout(update, timeout);3. The ClearScreen Function
This function is responsible for clearing the canvas and resetting the background color before each frame of the animation.
function clearScreen() {
gl.fillStyle = "blue"; // Set background color to blue
gl.fillRect(0, 0, width, height); // Fill the entire canvas with the color
gl.fill(); // Apply the fill
}
To use the clear function, we must call it the update function as shown below:
function update() {
clearScreen(); // Clear the screen before drawing
setTimeout(update, timeout);
}3. Helper functions
For this code to work, we need some helper functions to assist us. We will need point and line functions to draw the lines and points on the screen.
The Point Function
The point() function is responsible for drawing a 2D point (which represents a 3D point after projection) on the canvas.
function point(x, y, radius = 5, color = "white") {
gl.fillStyle = color; // Set the color for the point
gl.beginPath(); // Start a new drawing path
gl.arc(x, y, radius, 0, 2 * Math.PI, true); // Draw a circle (point) at (x, y)
gl.fill(); // Fill the circle with the chosen color
gl.closePath(); // Close the drawing path
}
The line Function
The line() function draws a 2D line between two points, helping us visualize edges between the 3D points after projection.
function line(x1, y1, x2, y2, width = 2, color = "white") {
gl.strokeStyle = color; // Set the color for the line
gl.lineWidth = width; // Set the width of the line
gl.beginPath(); // Start a new drawing path
gl.moveTo(x1, y1); // Move to the start point
gl.lineTo(x2, y2); // Draw a line to the end point
gl.stroke(); // Apply the stroke to render the line
}
4. The Vector Class
The vector class represents a point in 3D space. It has methods to rotate, scale, and project the point onto the 2D canvas.
// the vector class to represent a 3D vector (point)
class vector {
constructor(x, y, z) {
this.x = x; // x-coordinate
this.y = y; // y-coordinate
this.z = z; // z-coordinate
}
// Convert a 3D point to a 2D point for drawing
get_point2d() {
return project3Dto2D(this.x, this.y, this.z);
}
// Draw the point on the canvas
draw() {
var pt2d = this.get_point2d(); // Get the 2D coordinates
point(pt2d.x, pt2d.y); // Draw the point on the canvas
}
// Rotate the vector around the X-axis
rotateX(theta) {
const cosTheta = Math.cos(theta);
const sinTheta = Math.sin(theta);
const yNew = this.y * cosTheta - this.z * sinTheta;
const zNew = this.y * sinTheta + this.z * cosTheta;
this.y = yNew;
this.z = zNew;
}
// Rotate the vector around the Y-axis
rotateY(theta) {
const cosTheta = Math.cos(theta);
const sinTheta = Math.sin(theta);
const xNew = this.x * cosTheta + this.z * sinTheta;
const zNew = -this.x * sinTheta + this.z * cosTheta;
this.x = xNew;
this.z = zNew;
}
// Rotate the vector around the Z-axis
rotateZ(theta) {
const cosTheta = Math.cos(theta);
const sinTheta = Math.sin(theta);
const xNew = this.x * cosTheta - this.y * sinTheta;
const yNew = this.x * sinTheta + this.y * cosTheta;
this.x = xNew;
this.y = yNew;
}
// Scale the vector by a factor relative to the center
scale(scaleFactor, center) {
this.x = (this.x - center.x) * scaleFactor + center.x;
this.y = (this.y - center.y) * scaleFactor + center.y;
this.z = (this.z - center.z) * scaleFactor + center.z;
}
}
- Constructor: Initializes a vector with x, y, and z coordinates.
- get_point2d(): Projects the 3D vector onto a 2D plane using the
project3Dto2Dfunction. - draw(): Draws the vector as a point on the canvas.
- rotateX(), rotateY(), rotateZ(): Methods to rotate the vector around each axis.
- scale(): Scales the vector relative to a center point.
The project3Dto2D Function
This function is responsible for projecting 3D points onto a 2D canvas, using a simple perspective projection formula.
function project3Dto2D(x, y, z) {
let x2D = (x / (z + D)) * f + width / 2;
let y2D = -(y / (z + D)) * f + height / 2;
return { x: x2D, y: y2D }; // Return the 2D coordinates
}
Understanding 3D Rotation
Let’s also understand the basic concept of rotating points in 3D space used for the rotation functions. There are three main types of rotations in 3D space:
- Rotation around the X-axis
- Rotation around the Y-axis
- Rotation around the Z-axis
Rotation Around the X-axis
When a point rotates around the X-axis, the x-coordinate remains the same, while the y and z coordinates change. The rotation is defined by an angle, often called theta (θ), which tells how much the point is rotated.
The rotation matrix for the X-axis is:
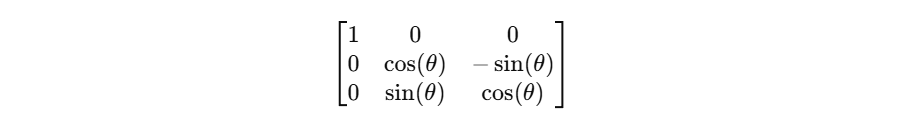
This means for a point (x,y,z), the new coordinates will be:
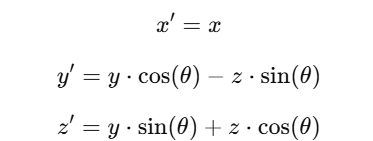
Rotation Around the Y-axis
Rotation around the Y-axis affects the x and z coordinates, while the y-coordinate remains unchanged.
The rotation matrix for the Y-axis is:
This means for a point (x,y,z), the new coordinates will be:
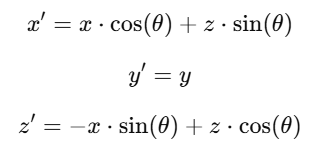
Rotation Around the Z-axis
Rotation around the Z-axis affects the x and y coordinates, while the z-coordinate remains unchanged.
The rotation matrix for the Z-axis is:
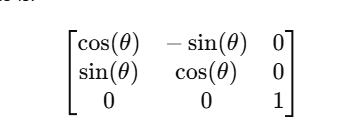
This means for a point (x,y,z), the new coordinates will be:
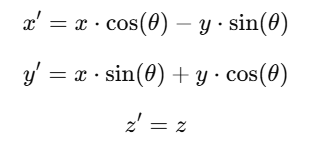
The Scaling Function
For the scale function, it takes two parameters: scaleFactor and center. The scaleFactor determines how much larger or smaller the point should become. A value greater than 1 will enlarge the point, while a value less than 1 will shrink it. The center parameter represents the point around which the scaling occurs. Typically, this could be the center of the object or a particular reference point in the 3D space.
5. The Model Class
The model class represents a 3D object made up of multiple points and edges. It allows for transformations like rotation and scaling.
// Class to represent a 3D model (collection of points and edges)
class model {
constructor(name, points, edges = []) {
this.name = name; // Name of the model
this.points = points; // Array of 3D points
this.edges = edges; // Array of edges connecting the points
}
// Draw the model on the canvas
draw() {
// First, draw the points
for (let i = 0; i < this.points.length; i++) {
this.points[i].draw(); // Draw each point using the draw method from the vector class
}
// Then, draw the edges connecting the points
for (let i = 0; i < this.edges.length; i++) {
var start = this.edges[i][0].get_point2d(); // Start point of the edge
var end = this.edges[i][1].get_point2d(); // End point of the edge
line(start.x, start.y, end.x, end.y); // Draw the line between the two points
}
}
// Rotate the model around the X-axis
rotateX(theta) {
theta = theta * Math.PI / 180;
for (let i = 0; i < this.points.length; i++) {
this.points[i].rotateX(theta);
}
}
// Rotate the model around the Y-axis
rotateY(theta) {
theta = theta * Math.PI / 180;
for (let i = 0; i < this.points.length; i++) {
this.points[i].rotateY(theta);
}
}
// Rotate the model around the Z-axis
rotateZ(theta) {
theta = theta * Math.PI / 180;
for (let i = 0; i < this.points.length; i++) {
this.points[i].rotateZ(theta);
}
}
// Scale the model by a factor relative to the center of the model
scale(scaleFactor) {
// Find the center of the model
const center = this.getCenter();
// Scale all points relative to the center
for (let i = 0; i < this.points.length; i++) {
this.points[i].scale(scaleFactor, center);
}
}
// Get the center of the model by averaging all points
getCenter() {
let centerX = 0, centerY = 0, centerZ = 0;
for (let i = 0; i < this.points.length; i++) {
centerX += this.points[i].x;
centerY += this.points[i].y;
centerZ += this.points[i].z;
}
return new vector(centerX / this.points.length, centerY / this.points.length, centerZ / this.points.length);
}
}- Constructor: Initializes a model with a name, points (3D vectors), and edges (connections between points).
- draw(): Loops through all points and edges to render the model.
- rotateX(), rotateY(), rotateZ(): Rotate all points of the model around the respective axes.
- scale(): Scales the entire model relative to its center.
6. Model Instance
We can create an instance of the model class to represent our 3D cube. The cube is defined by its vertices (points) and the edges connecting them.
// Define the points for the cube model (8 vertices of a cube in 3D space)
const points = [
vec(-100, -100, -100), // Bottom-left-front
vec(100, -100, -100), // Bottom-right-front
vec(100, 100, -100), // Top-right-front
vec(-100, 100, -100), // Top-left-front
vec(-100, -100, 100), // Bottom-left-back
vec(100, -100, 100), // Bottom-right-back
vec(100, 100, 100), // Top-right-back
vec(-100, 100, 100) // Top-left-back
];
// Define the edges connecting the points to form a cube (12 edges)
const edges = [
[points[0], points[1]], [points[1], points[2]], [points[2], points[3]], [points[3], points[0]], // Bottom face
[points[4], points[5]], [points[5], points[6]], [points[6], points[7]], [points[7], points[4]], // Top face
[points[0], points[4]], [points[1], points[5]], [points[2], points[6]], [points[3], points[7]] // Sides
];
mdl = create_model("cube", points, edges);
mdl.scale(1); // Initial scaling of the model
7. Draw and Add Animations
Finally, lets draw the model within the update loop and animate it with some rotates:
// Function to update the canvas, clear the screen, and draw the model
function update() {
clearScreen(); // Clear the screen before drawing
// Create the model using the points and edges defined above
mdl.rotateY(10);
// Draw the model
mdl.draw();
// Continuously update the canvas at the specified timeout interval
setTimeout(update, timeout);
}Bonus: Visualizing a 4D Tesseract (Hypercube) in 3D
New Variables for 4D Projection
To handle the extra dimension, we've modified the vector class to include a new fourth dimension, w. The project4Dto3D function is responsible for projecting a 4D point (x, y, z, w) to 3D space using perspective projection.
function project4Dto3D(x, y, z, w) {
let x3D = (x / (w + D)) * f + width / 2;
let y3D = (y / (w + D)) * f + height / 2;
let z3D = (z / (w + D)) * f;
return { x: x3D, y: y3D, z: z3D };
}
Rotation of 4D Tesseract
The Tesseract is a four-dimensional object, and visualizing it requires rotating it in multiple dimensions. We added an extra rotation method, rotateW(), to handle the rotation of the Tesseract along its 4th dimension.
class vector {
constructor(x, y, z, w) {
this.x = x;
this.y = y;
this.z = z;
this.w = w;
}
get_point3d() {
return project4Dto3D(this.x, this.y, this.z, this.w);
}
draw() {
var pt3d = this.get_point3d();
point(pt3d.x, pt3d.y);
}
rotateW(theta) {
const cosTheta = Math.cos(theta);
const sinTheta = Math.sin(theta);
const zNew = this.z * cosTheta - this.w * sinTheta;
const wNew = this.z * sinTheta + this.w * cosTheta;
this.z = zNew;
this.w = wNew;
}
rotateX(theta) {
const cosTheta = Math.cos(theta);
const sinTheta = Math.sin(theta);
const yNew = this.y * cosTheta - this.z * sinTheta;
const zNew = this.y * sinTheta + this.z * cosTheta;
this.y = yNew;
this.z = zNew;
}
rotateY(theta) {
const cosTheta = Math.cos(theta);
const sinTheta = Math.sin(theta);
const xNew = this.x * cosTheta + this.z * sinTheta;
const zNew = -this.x * sinTheta + this.z * cosTheta;
this.x = xNew;
this.z = zNew;
}
rotateZ(theta) {
const cosTheta = Math.cos(theta);
const sinTheta = Math.sin(theta);
const xNew = this.x * cosTheta - this.y * sinTheta;
const yNew = this.x * sinTheta + this.y * cosTheta;
this.x = xNew;
this.y = yNew;
}
}rotateW(theta) {
const cosTheta = Math.cos(theta);
const sinTheta = Math.sin(theta);
const zNew = this.z * cosTheta - this.w * sinTheta;
const wNew = this.z * sinTheta + this.w * cosTheta;
this.z = zNew;
this.w = wNew;
}
Drawing and Animating the Tesseract
The Tesseract is defined by 16 points in 4D space and 32 edges connecting them. We use the model class to store and render these points and edges. The update function rotates the Tesseract along the x, y, z, and w axes for a continuous animation.
mdl.rotateX(0.05);
mdl.rotateY(0.05);
mdl.rotateZ(0.05);
mdl.rotateW(0.05);
Conclusion
With this tutorial, you should be able to make your own 3D visualization using a web browser and JavaScript. You can experiment with different 3D visual ideas and see what you can create. We would love to see what you create. Feel free to leave comment below. Happy creative coding!
